“高等数学”专升本考试要求说明

考试范围：一元函数微积分学

参考教材：高等数学（第五版）上册  

作者：盛祥耀  主编  

出版社：高等教育出版社 ，

考试大纲：

第一章  函数极限连续

§1．1  函数

1．理解函数的概念，了解简单性质。

2．熟悉基本初等函数的性质和图形。

§1．2  极限的概念

1．了解极限的“

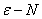”，“ ”的定义与极限的性质。

2．会求函数在一点的左、右极限。

3．了解函数在一点处极限存在的充分必要条件。

§1．3  极限运算

1．掌握极限的四则运算法则。

§1．4  无穷小量的比较

1．理解无穷小、无穷大的概念。

2．掌握无穷小的性质、无穷小与无穷大的关系。

3．会进行无穷小阶的比较（高阶、低阶、同阶和等价）。

4．会运用等价无穷小代换求极限。

5．熟练掌握用两个重要极限求极限的方法。

§1．5 函数的连续性

1．理解函数在一点连续与间断的概念。

2．理解函数在一点处连续与极限存在的关系。

3．掌握判断函数（含分段函数）在一点处连续的方法。

4．会求函数的间断点。

5．掌握在闭区间上连续函数的性质，会用介值定理推证一些简单命题。

6．理解初等函数在其定义区间上连续，会利用函数连续性求极限。

第二章  导数与微分

§2．1  导数的概念

1．理解导数的概念及其几何意义。

2．掌握函数可导性与连续性的关系。

3．会用导数定义求一些简单函数的导数。

4．会求曲线上一点的切线方程与法线方程。

§2．2  函数的微分法

1． 熟练掌握导数的基本公式、四则运算法则及复合函数的求导法则。

2． 了解函数的反函数的求导法则。

3． 会求初等函数的导数。

4． 会求分段函数的导数。

§2．3  函数的微分及其应用

1． 理解微分的概念，了解可导与可微的关系。

2． 掌握微分法则, 会用微分法则及一阶微分形式不变性求函数的微分。

§2．4  隐函数及由参数方程所确定的函数的微分法

1． 掌握隐函数的求导法、对数求导法。

2． 掌握由参数方程所确定的函数的求导方法,。

§2．5  高阶导数

1． 理解高阶导数的概念。

2． 会求简单函数的n阶导数。

第三章 导数的应用

§3．1  微分中值定理及洛必达法则

1． 理解罗尔定理、拉格朗日中值定理及它们的几何意义。

2． 会用罗尔定理证明方程根的存在性。

3． 会用拉格朗日中值定理证明简单的不等式。

4． 熟练掌握用洛必达法则求0/0、¥/¥、0×¥ 、¥－¥ 、0⁰ 、1^¥ 、¥⁰型未定式的极限的方法。

§3．2  函数的单调性及其极值

1． 掌握利用导数判定函数的单调性及求函数单调增、减区间的方法。

2． 会利用函数的单调增减性证明简单的不等式。

3． 理解函数极值的概念，掌握求函数极值的方法。

§3．3  函数的最大值和最小值

1． 掌握求函数最大值与最小值的方法。

2． 会解简单的应用问题。

§3．4  曲线的凹凸性与拐点、函数图形的描绘

1． 会判定曲线的凹凸性，会求曲线的拐点。

2． 会求曲线的水平渐近线与铅垂渐近线。

3． 会作出简单函数的图形。

第四章 不定积分

§4．1  不定积分的概念与性质

1． 理解原函数与不定积分的概念及其关系。

2． 掌握不定积分的性质。

3． 了解原函数的存在定理。

4． 熟练掌握不定积分的基本公式。

§4．2  换元积分法

1． 熟练掌握不定积分第一换元法。

2． 掌握第二换元法（限于三角代换与简单根式代换）。

§4．3  分部积分法

1． 熟练掌握不定积分的分部积分法。

第五章 定积分

§5．1  定积分的概念与性质

1．理解定积分的概念及其几何意义，了解函数可积的条件。

2．掌握定积分的基本性质。

§5．2  微积分的基本公式

1．理解变上限的定积分是变上限的函数，掌握对变上限积分求导方法。

2．熟练掌握牛顿(Newton)－莱布尼兹（Leibniz）公式。

§5．3  定积分的换元积分法与分部积分法

1．掌握定积分的换元法。

2．理解定积分的对称性，会利用对称性简化计算定积分。

3．掌握定积分的分部积分法。

§5．4  反常积分

1．理解无穷区间的反常积分的概念。

2．掌握无穷区间的反常积分的计算方法。

第六章 定积分的应用

§6．1  定积分的微元法

1．理解定积分微元法的思想及其概念。

§6．2  平面图形的面积

1．掌握直角坐标系下用定积分计算平面图形的面积。

§6．3  旋转体的体积

1．掌握直角坐标系下用定积分计算平面图形绕坐标轴旋转所生成的旋转体的体

积。